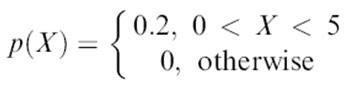VARIABEL RANDOM
VARIABEL RANDOM (VR) pada dasarnya adalah bilangan random.
Misalkan kita melempar 3 koin, maka ruang sampelnya adalah:
Ω = {hhh, hht, htt, hth, ttt, tth, thh, tht}
Beberapa contoh variabel random:
banyaknya muncul muka.
banyaknya muncul belakang
selisih antara banyak muka dan banyak belakang.
Secara matematis, v.r. adalah fungsi X : Ω -> R. Karena karena
kejadian pada ruang sampel Ω random (acak) maka bilangan yang
dihasilkan oleh nilai fungsi X juga acak. Perhatikan contoh di atas:
X1: Ω -> R dimana X1(hhh) = 3, X1(hth) = 2, X1(tth)=1, X1(ttt)=0,
ditulis X1 ∈ {0, 1, 2, 3} himp semua kemungkinan nilai X1.
2. Coba ilustrasikan untuk contoh 2 dan 3.
V.r. yang nilai-nilainya berupa himp diskrit disebut v.r. diskrit.
DISTRIBUSI PROBABILITAS
1.diskrit
CONTOH: Misalkan sepasang dadu dilempar dan X menyatakan
jumlah angka yang muncul. Maka VR X mempunyai nilai {2, 3, . . . , 12}.
Bahwa X bernilai 5 terjadi pada kasus (1,4), (2,3), (3,2), (4,1). Jadi
P(X=5) = 4/36 = 1/9.
Distribusi probabilitas vs Distribusi frekuensi-relatif
Distribusi probabilitas merupakan distribusi frekuensi relatif yang ideal atau secara teoritis.
2. KONTINU
Bila nilai v.r. X berjalan pada himpunan kontinu (takterhitung) maka kurva y = p(X) berupa kurva dan untuk X=x, p(x) didef sbg probabilitas bahwa X=x, ditulis
p(x) = Prob(X=x). Notasi p(a
Misalkan v.r. X mempunyai nilai diantara 0 dan 5 dengan
a. Buktikan p adalah fungsi kepadatan peluang?
b. Hitunglah probabilitas bahwa X terletak diantara 2.5 dan 4.
Ekspektasi Matematika
- Merupakan nilai harapan teoritis yang ditentukan oleh peluang terjadinya nilai tertentu suatu v.r. Ilustrasi: misalkan anda mempunyai peluang 0.25 untuk mendapatkan uang 1 juta maka nilai ekspektasi anda adalah 0.25 x 1 juta = 250 ribu.
- Secara umum, bila v.r. X mempunyai kemung-kinan nilai X1, X2, . . . Xk dengan masing-masing peluang X bernilai Xk adalah pk maka nilai harapan X, ditulis E(X) didefinisikan sbg:
- Probabilitas pk dapat diganti dengan frek.-relatif
-Contoh: Misalkan v.r. diskrit X mempunyai distribusi prob. berikut:
a. Tunjukkan kebenaran bahwa p fungsi distribusi.
b. Hitunglah E(X).
PERUMUSAN:
E(Xk) = Σ Xk p(X)
E(X-a)k = Σ (X-a)k p(X)
Bila a = maka dapat ditunjukkan E(X- )2 adalah
variansi.
CONTOH:
Misalkan v.r. X mempunyai distri probabilitas sbb:
TUGAS
Supplementary problems:
6.40 – 6.80
MISCELLANEOUS PROBLEMS:
6.83 – 6.100
Harap dikerjakan mulai detik ini juga, jangan tunda menit berikutnya karena masih ada soal berikutnya dalam bentuk copian.
